Un simple oracle 2/2 (Cryptanalyse) - 404CTF 2022

Fichiers du challenge Principe:
Savoir que -1**d_premier mod N = N - 1 ce qui permet de déjouer l'oracle comme précédemment, même si celui-ci ne nous donne pas le module N

Le challenge

Même principe que Un simple oracle 1/2 (Cryptanalyse) , avec moins d'informations (script de résolution ici)

Byebye module

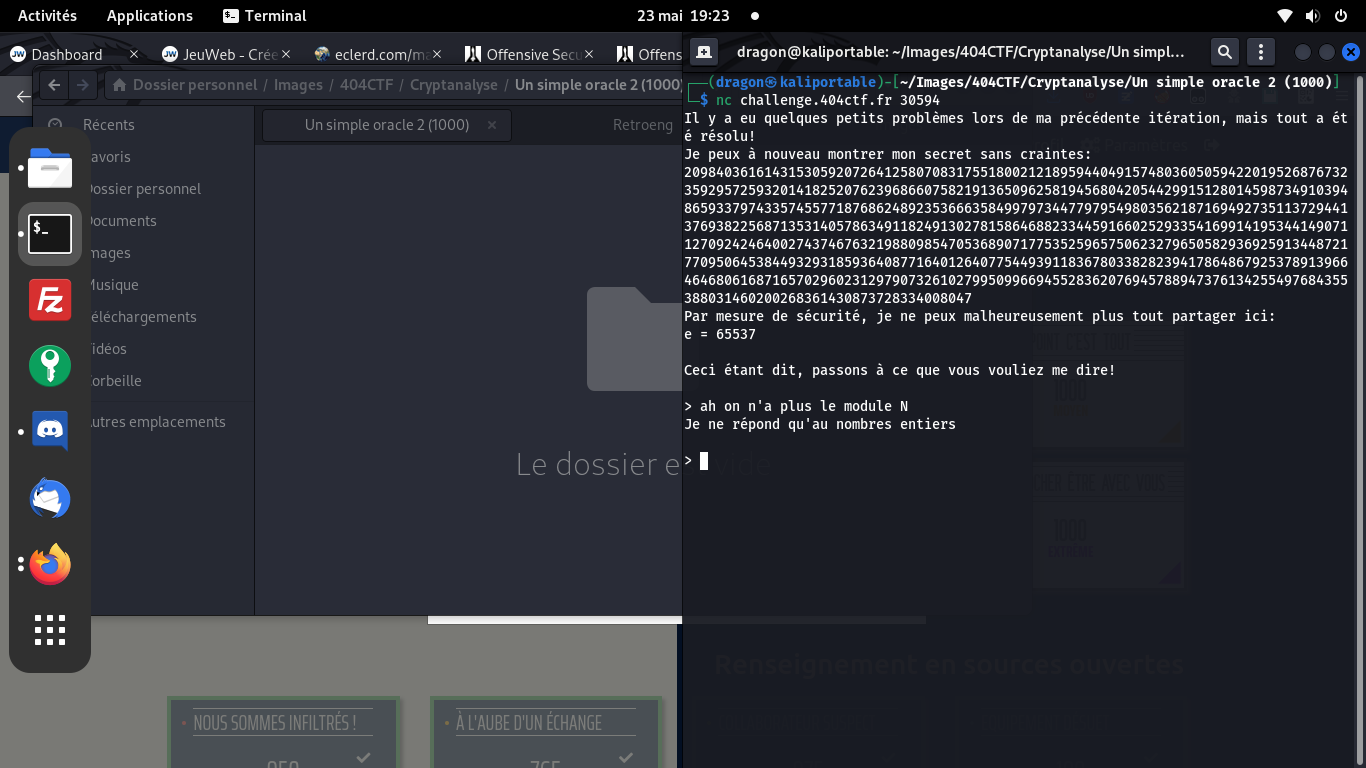
La différence avec l'oracle précédent est l'absence de module

Je vais sur la terrasse, je roupille un peu, et je me demande: que se passe-t-il si j'envoie -1 à l'oracle? Vu que 0 et 1 sont des valeurs un peu spéciale, -1 pourrait aussi l'être

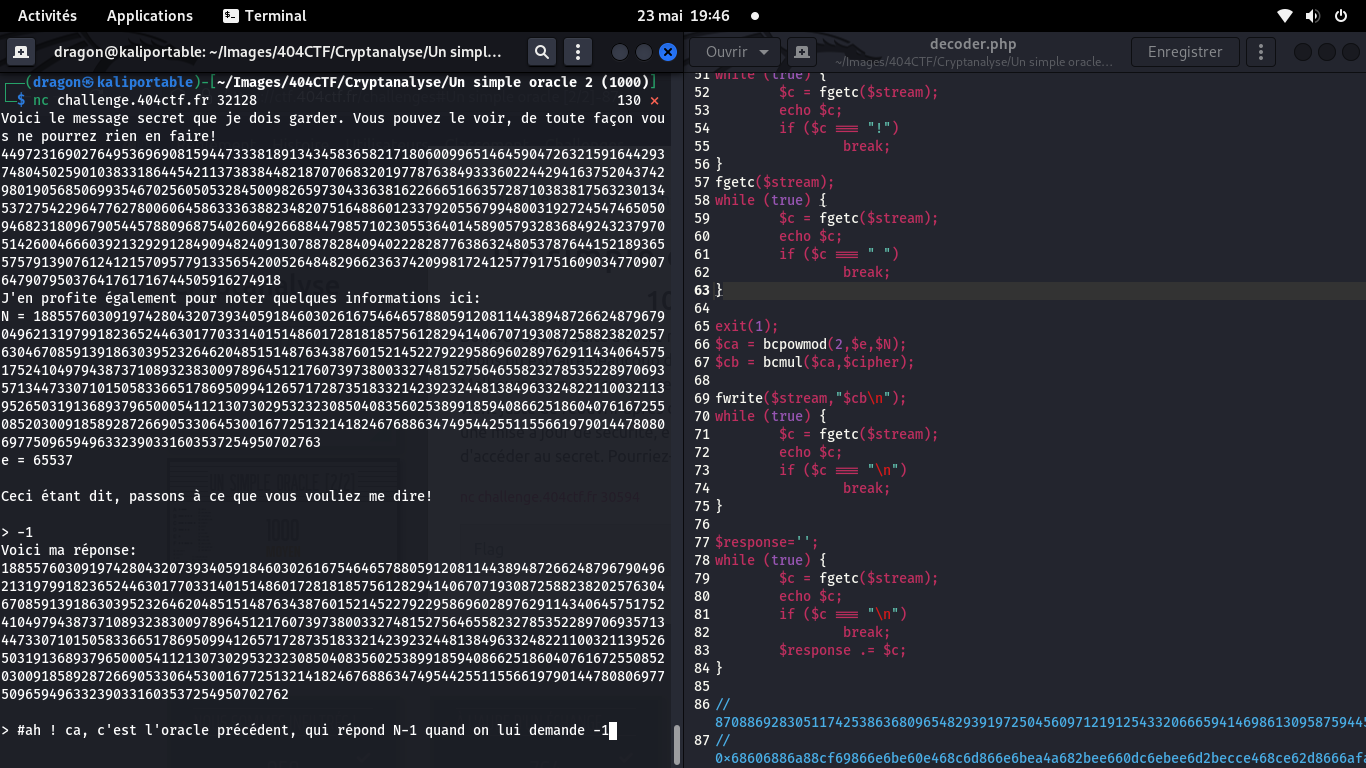
Je reprends donc l'oracle 1, et j'envoie -1 à l'oracle 1 (car celui-ci donne plus d'informations): l'oracle renvoie N - 1!

Quand des challenges sont ainsi liés, avec un second challenge similaire au premier mais donnant moins d'informations, faire ses tests sur le premier challenge (plus complet) est très pratique

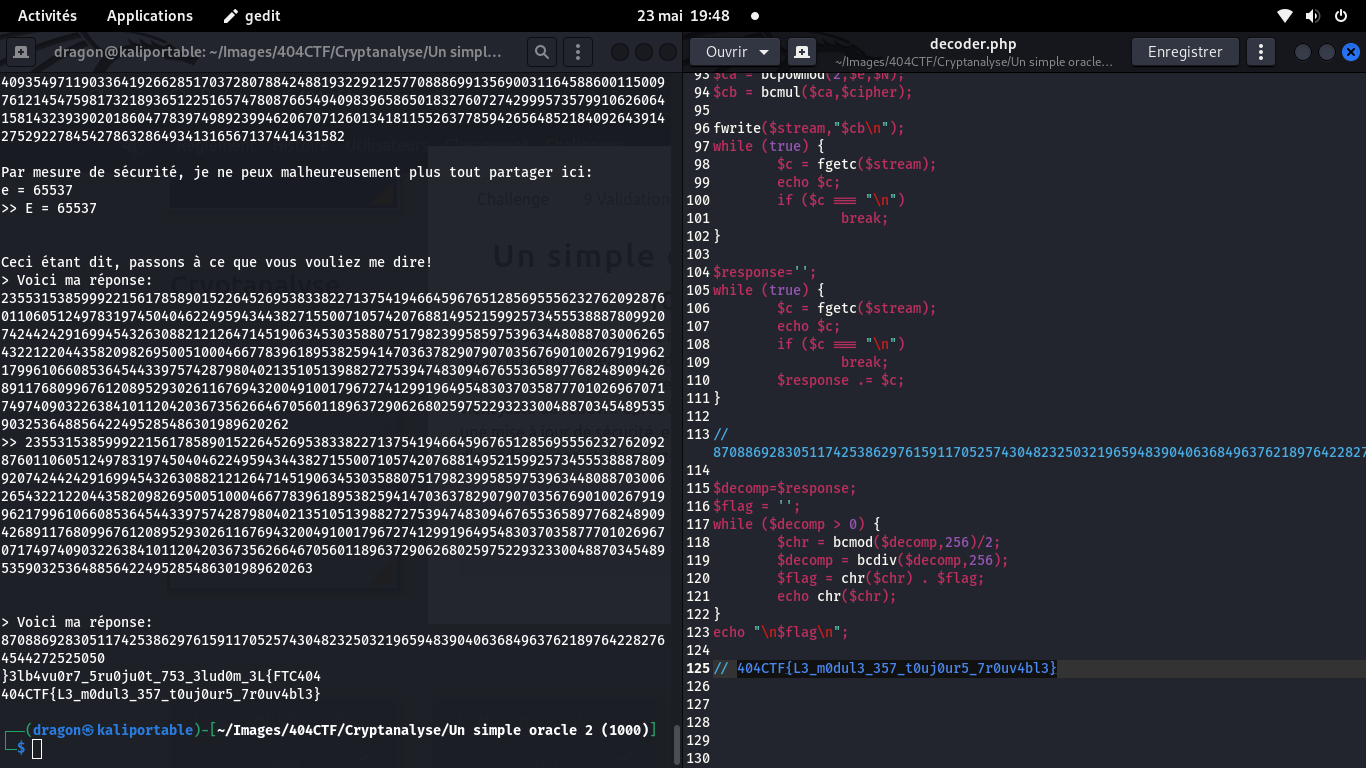
On garde donc le même code, en envoyant -1 à l'oracle d'abord pour récupérer le module N et poof, flag:
404CTF{L3_m0dul3_357_t0uj0ur5_7r0uv4bl3}

En pratique, cela marche car -1 ** [un nombre premier, donc impair] = -1 et car -1 mod N = N - 1 donc -1 ** d mod N = N - 1

Fichiers du challenge

⇇ 404CTF 2022