Principe:
Principe:
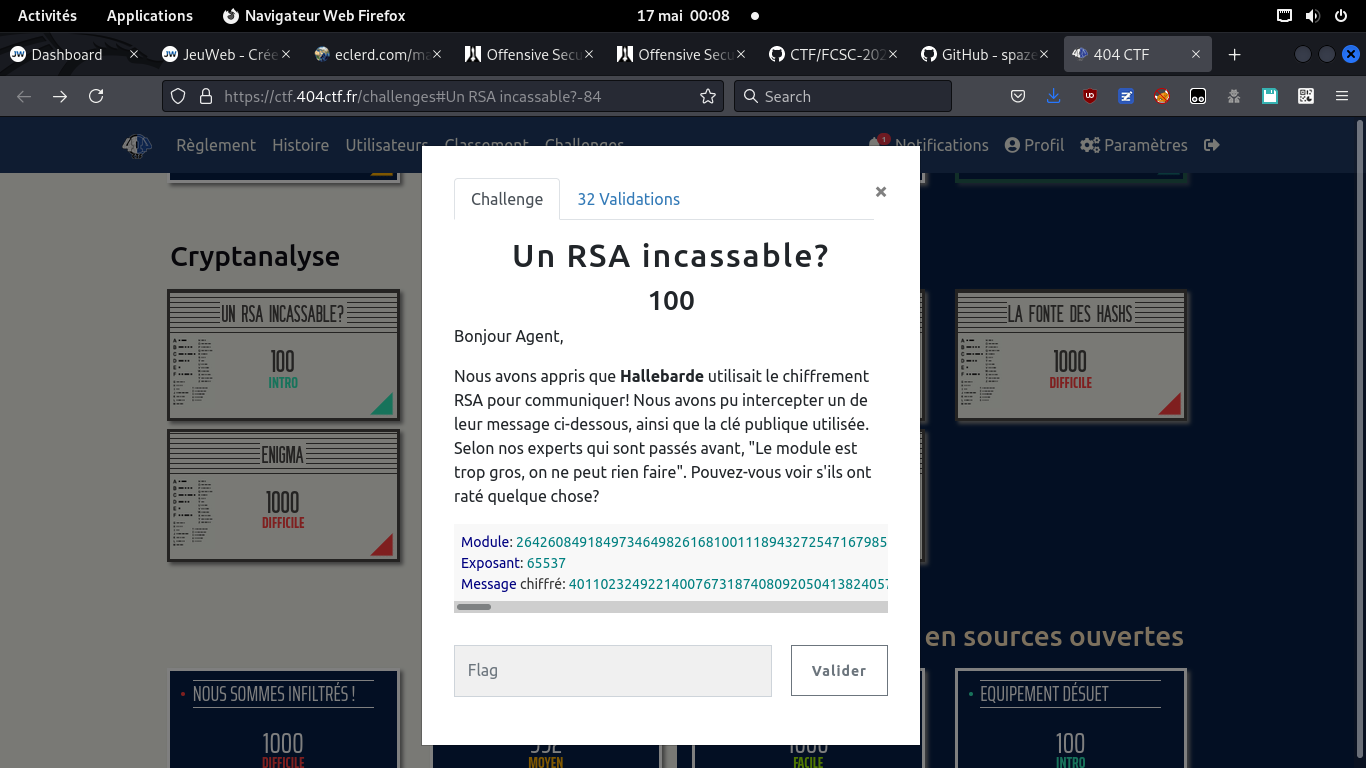
Factoriser le N d'un RSA pour trouver phi(N) et en déduire d, la clef de déchiffrement
Le "challenge"
RSA et factorisation
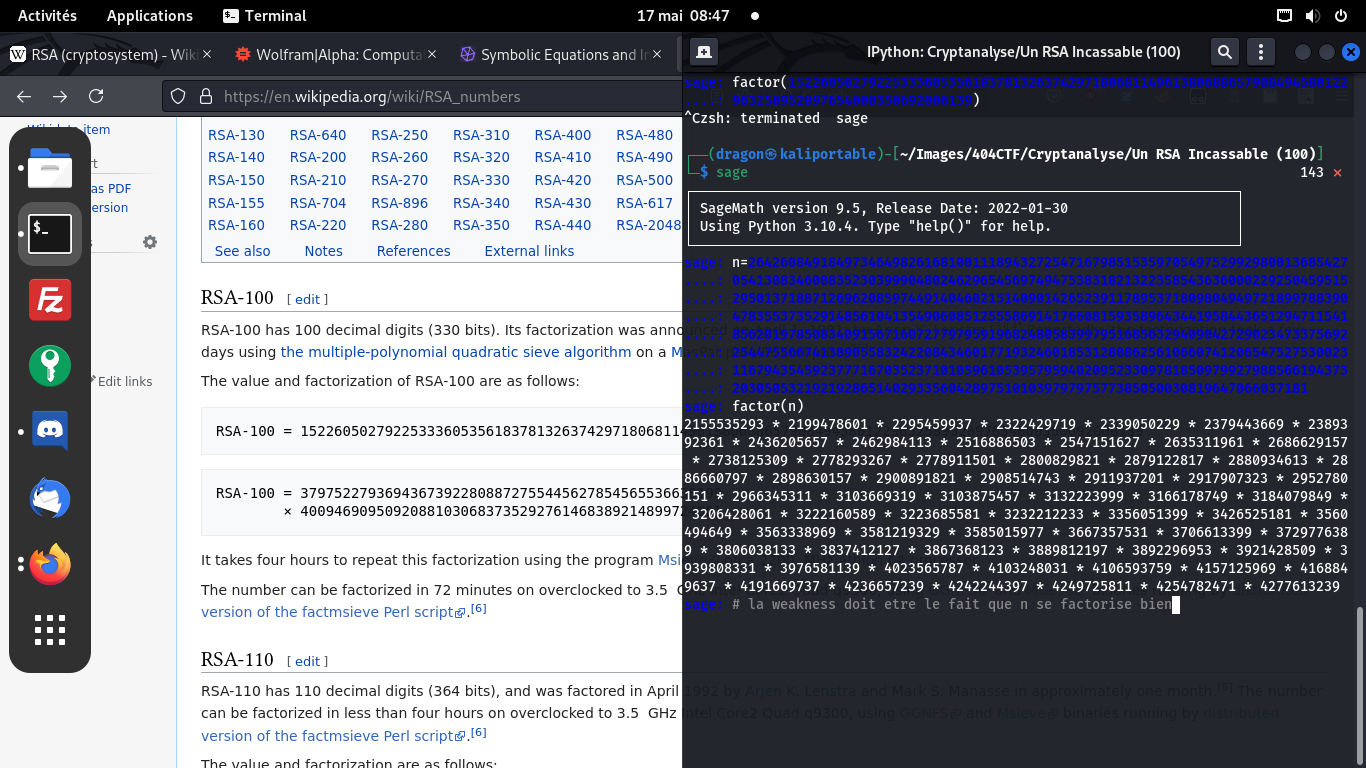
Sage est un équivalent open-source à Maple, très efficace pour faire du calcul symbolique (c'est à dire qu'il sait résoudre des équations, manipuler des inconnues et des variables, etc)
Normalement, pour que RSA soit sécurisé N ne doit pas être factorisable facilement et doit être le produit de deux grands nombres premiers. Ici, on a un N composé de nombreux facteurs, ce qui est totalement inhabituel (et ce qui explique la factorisation rapide)
Phi

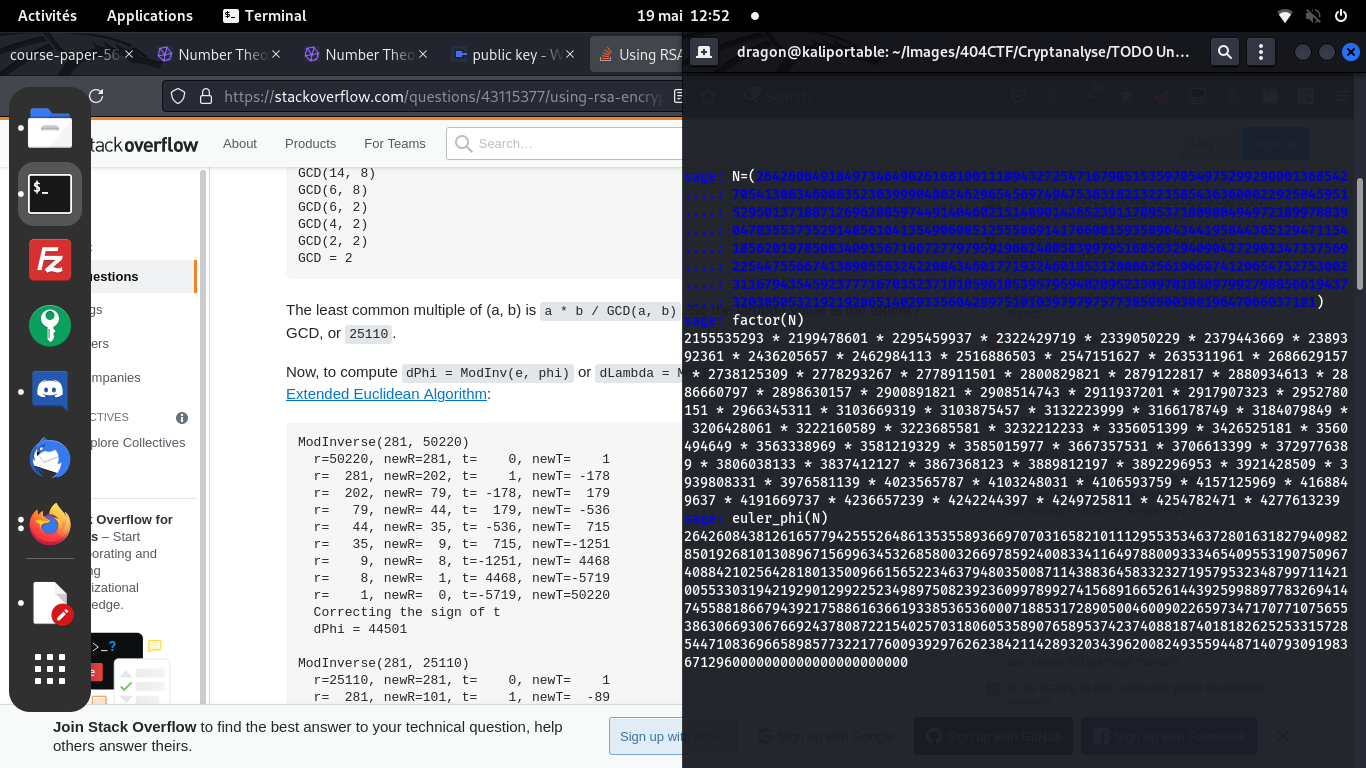
Notez que phi(A*B) = phi(A)*phi(B) d'où le fait que Sage puisse rapidement calculer phi(N). Si le calcul avait été long, on aurait pu utiliser la décomposition de N pour chaquer le phi de chacun de ses facteurs, et en faire ensuite le produit
d
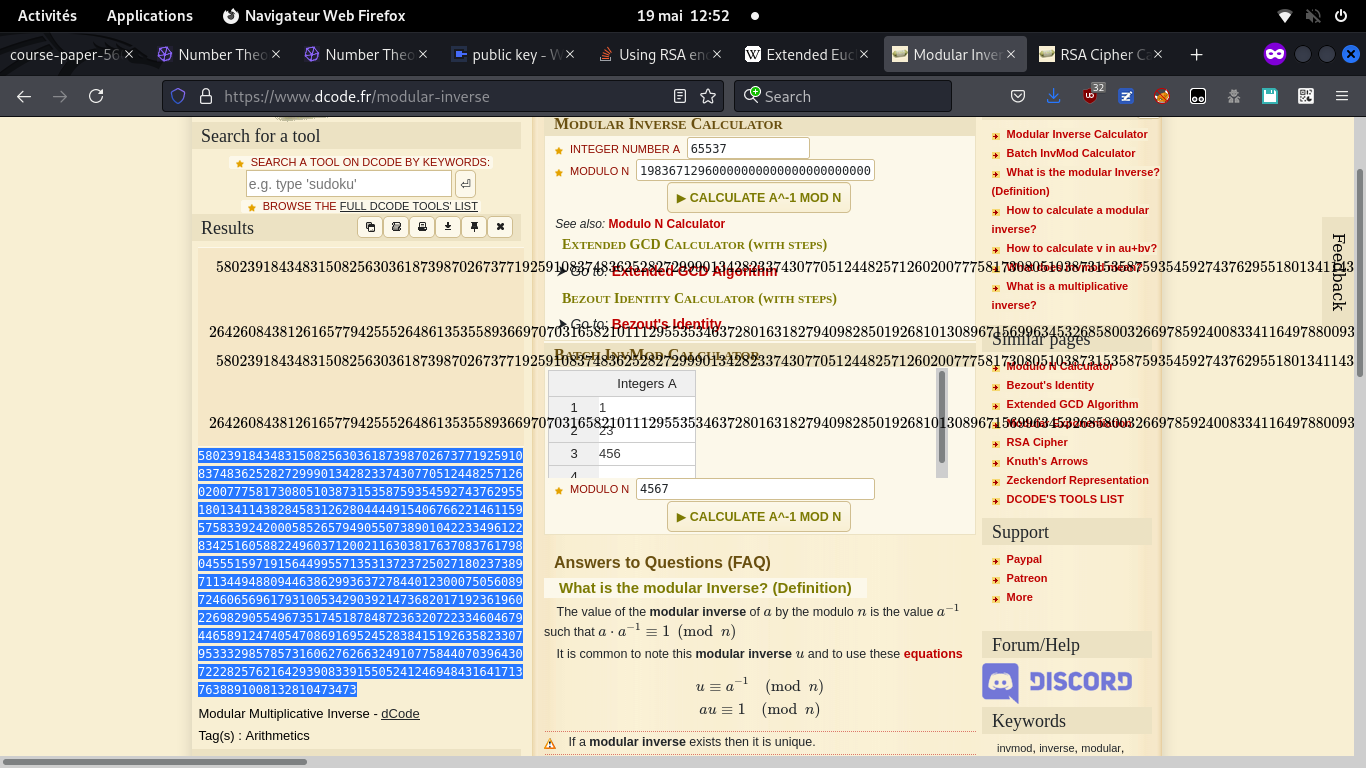
Flag
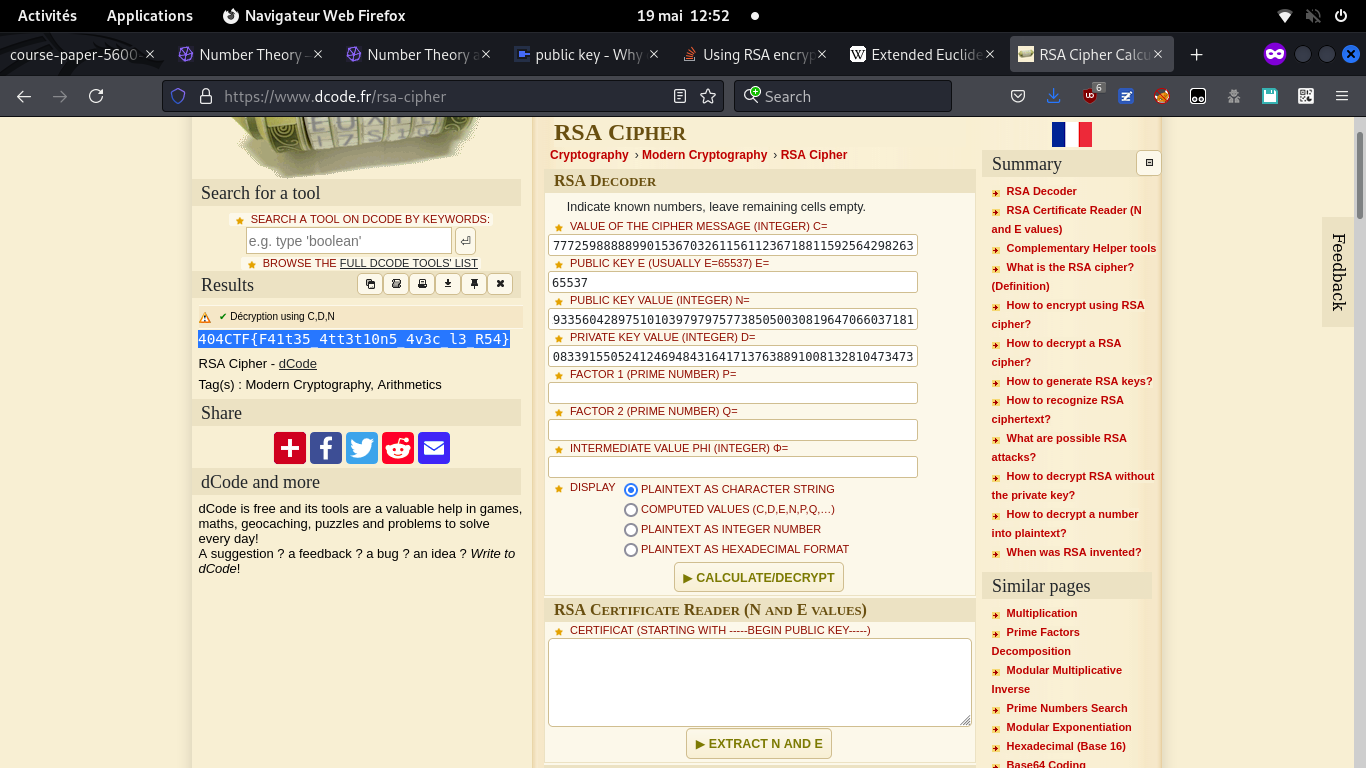
404CTF{F41t35_4tt3t10n5_4v3c_l3_R54}
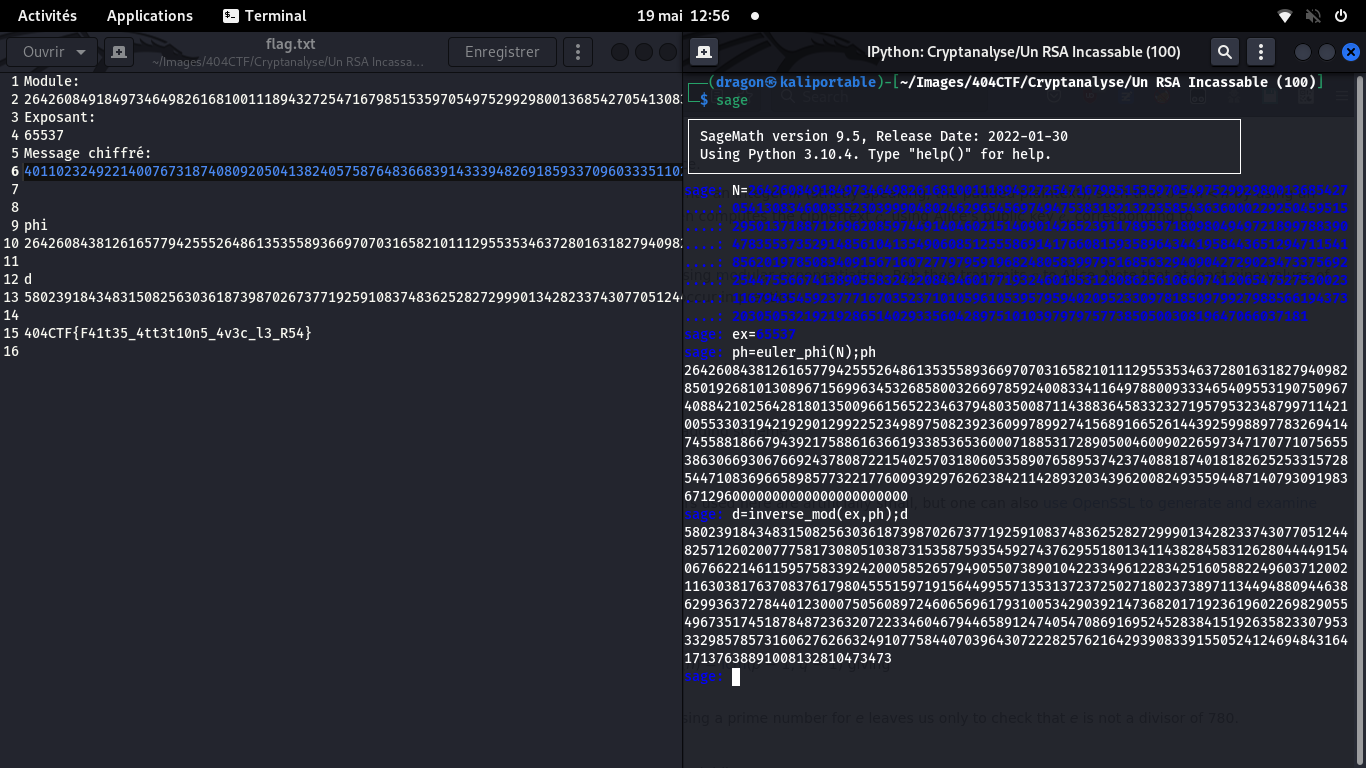
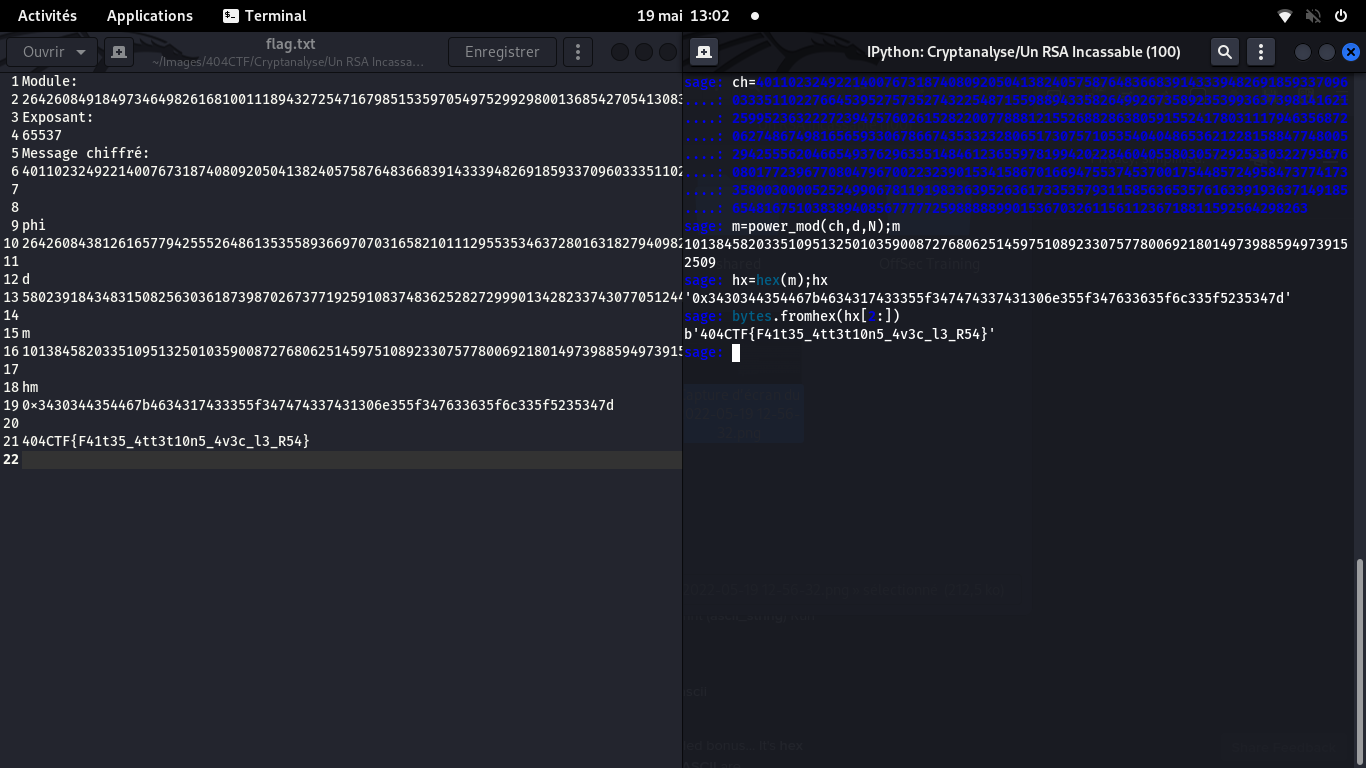
En pratique, en déchiffrant, on obtient un nombre m:
101384582033510951325010359008727680625145975108923307577800692180149739885949739152509
On le bascule en base 16:
0x3430344354467b4634317433355f347474337431306e355f347633635f6c335f5235347d
Et on converti chaque paire d'octets via la table ASCII
404CTF{F41t35_4tt3t10n5_4v3c_l3_R54}
Sage-only