 Principe:
Principe:
Exploiter un point fixe non-trivial du RSA (un message qui, chiffré, est égale à lui-même) pour factoriser N = P*Q et retrouver d, qui permet de déchiffrer le flag
Le challenge
Le challenge a été refait pendant le CTF car la factorisation de N avait leaké sur internet. Ce point sera important dans la résolution!
J'avais oublié de screener l'énoncé, alors je l'ai screené une fois le flag entré
Mise de côté
En voyant les données du challenge, je pensais qu'il s'agirait d'une timing attack: on a des données d'entrée, on a la valeur chiffrée et on a la durée de chiffrement et de déchiffrement. Je me disais donc qu'à partir de ça, j'aurai été capable de déterminer, bit à bit, la valeur de d sur la base de ces durée. Dans le concept, cela aurait été "si la durée de chiffrement de 00..010..0 est plus longue que celle de 00..001, alors il devrait y avoir un 1 en x-eme place de d
Mais dans l'un des autres challenges, appelé "Puisse Kocher être avec vous", la mention du nom de "Kocher" (lié aux side-channel attacks) m'a aussi murmuré à l'oreille que ce challenge ne serait peut-être pas une timing attack (sinon, les deux challenges seraient trop similaires).
Ne sachant par où partir, j'ai mis le challenge de côté. Jusqu'à ce que, sur Discord, les organisateurs annoncent que les données du challenge (et le flag) ont été renouvelés, car la factorisation de N avait fuitée sur FactorDB.
Fuite
404CTF{f1x3d_P01n75_4Re_v3ry_C00l}
Mon idée était de déchiffrer le flag précédent (qui me donnerait un indice), d'appliquer la méthode vers laquelle le flag me pointera aux anciennes données (dont je connais la solution du coup), puis de faire de même sur le nouveau challenge (pour flagger vraiment)
Points fixes
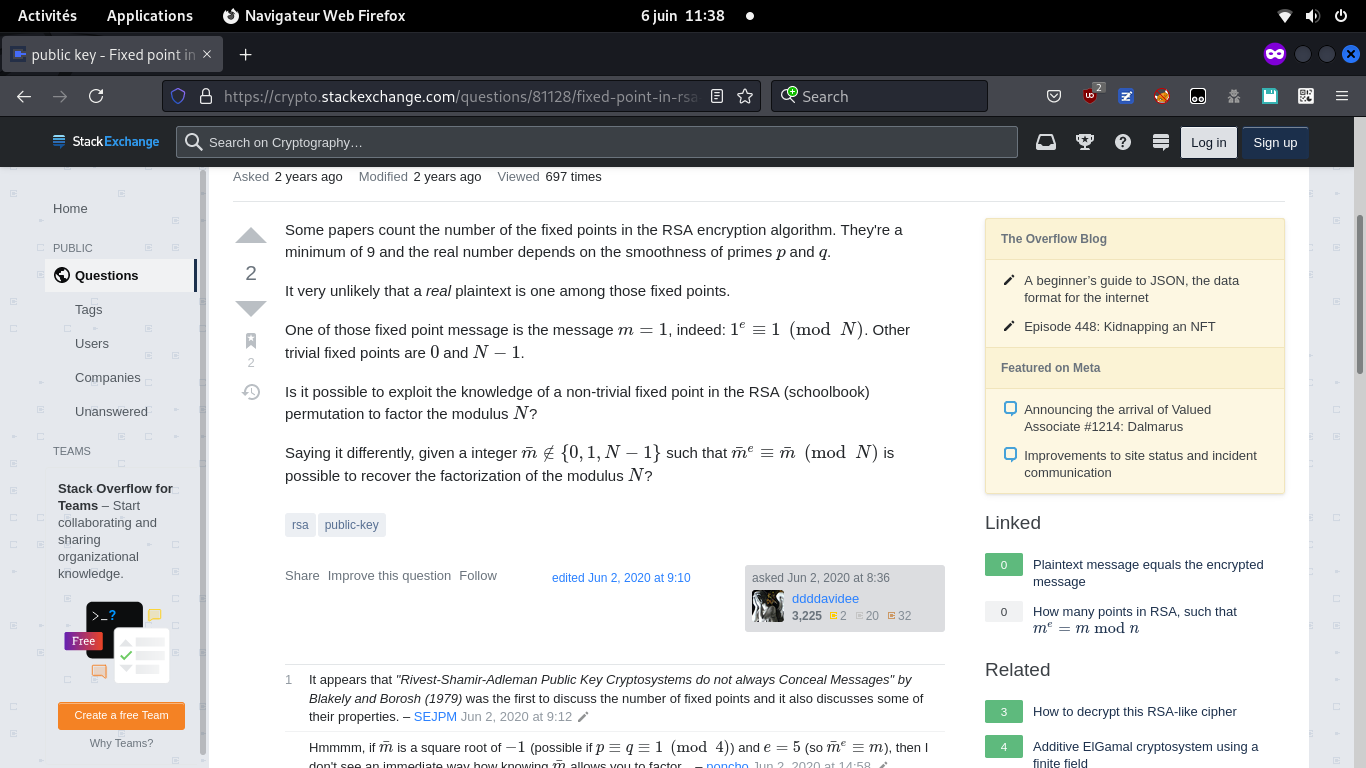
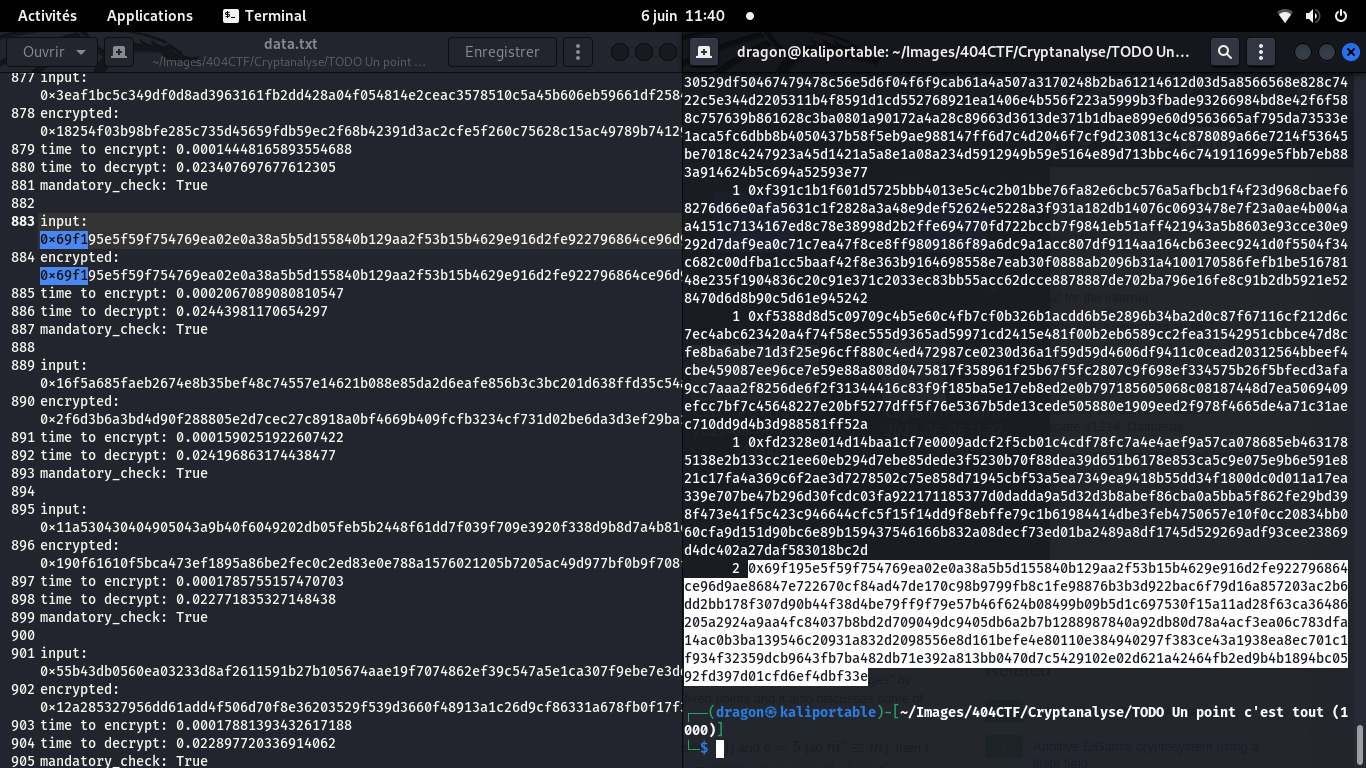
Si vous vous souvenez de Un simple oracle 1/2 (Cryptanalyse) , on savait déjà que 0 et 1 sont des points fixes pour toute clef RSA, appelés "points fixes triviaux".
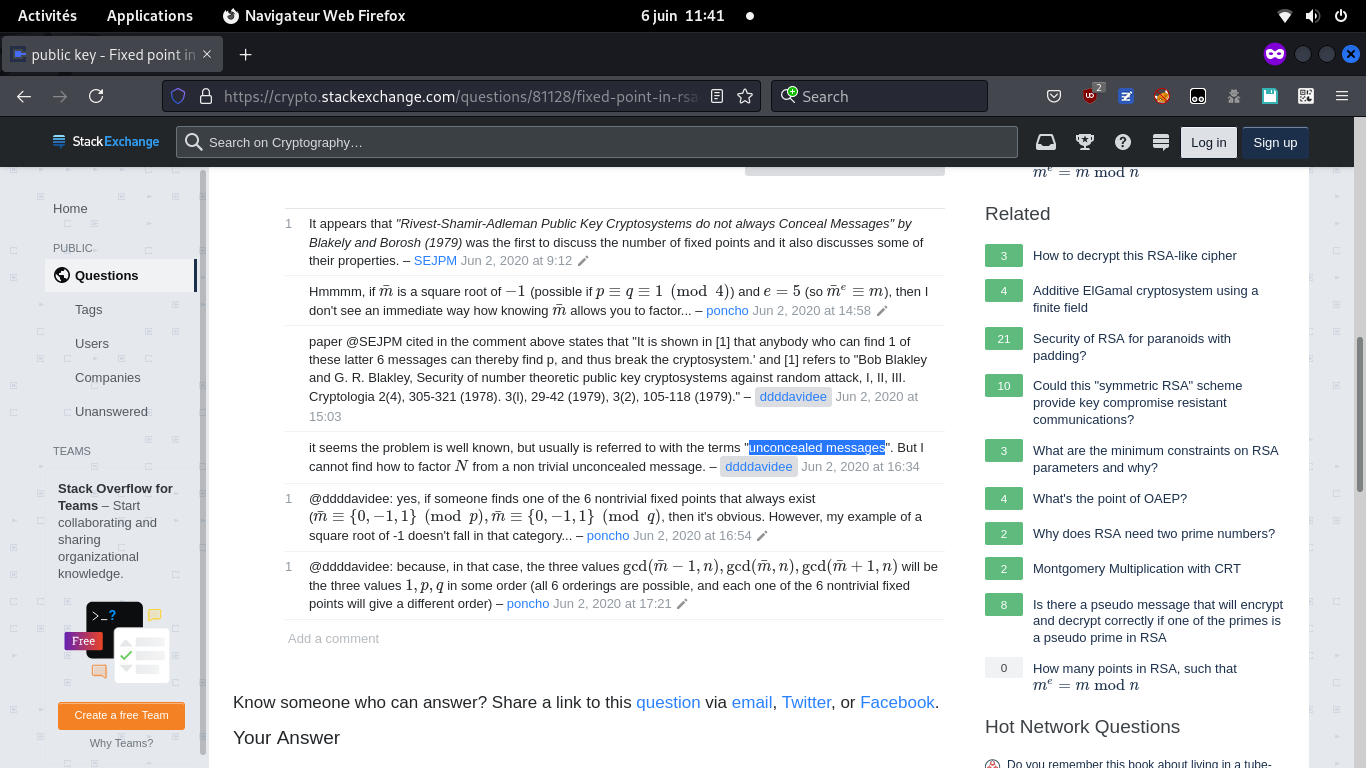
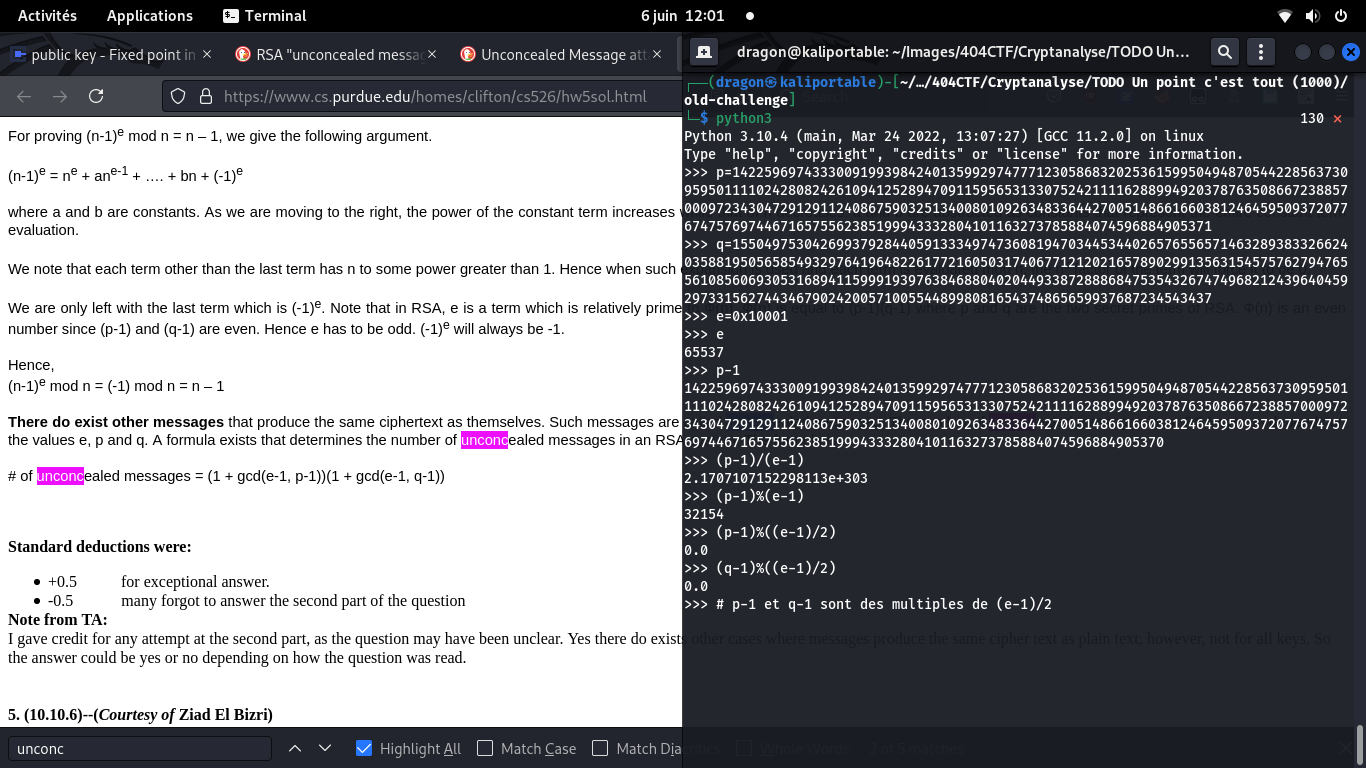
Cela nous renforce encore dans l'idée que ce point fixe est la solution, et que le challenge n'a donc rien à voir avec une timing attack
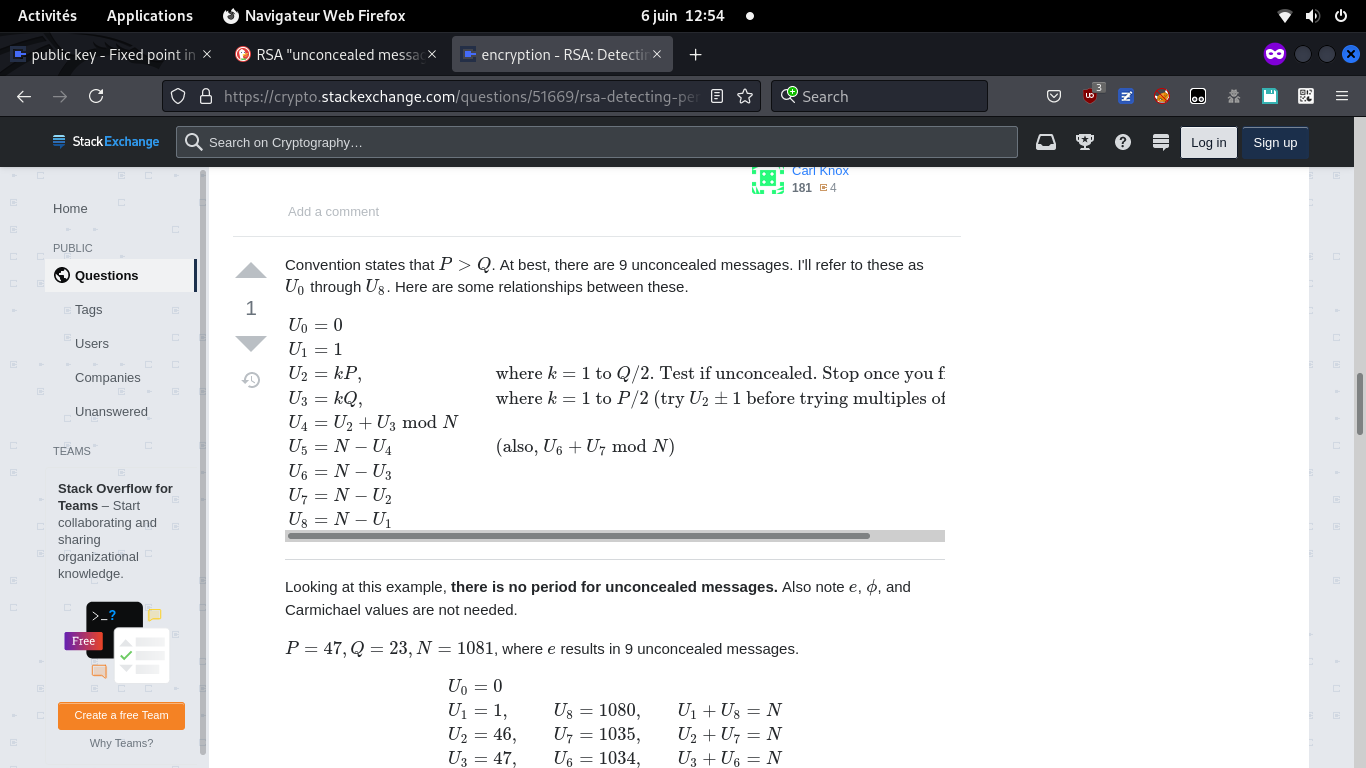
C'est là aussi une excellente piste, car cela expliquerait comment le challenge a été construit: à partir de P et Q, connus par le créateur du challenge, choisir les bonnes input pour obtenir un seul point fixe non trivial est simple
Cela fonctionne car u est un point fixe si et seulement si
u = {0,-1,1} mod P et u = {0,-1,1} mod Q.
Pour le point non trivial u = U2 = k*P = 0 mod P
alors u = {-1,1} mod Q car si on avait u = 0 mod Q alors u = k*P = k'*Q = N = 0 mod N
(P et Q premiers) donc u serait un point fixe trivial.
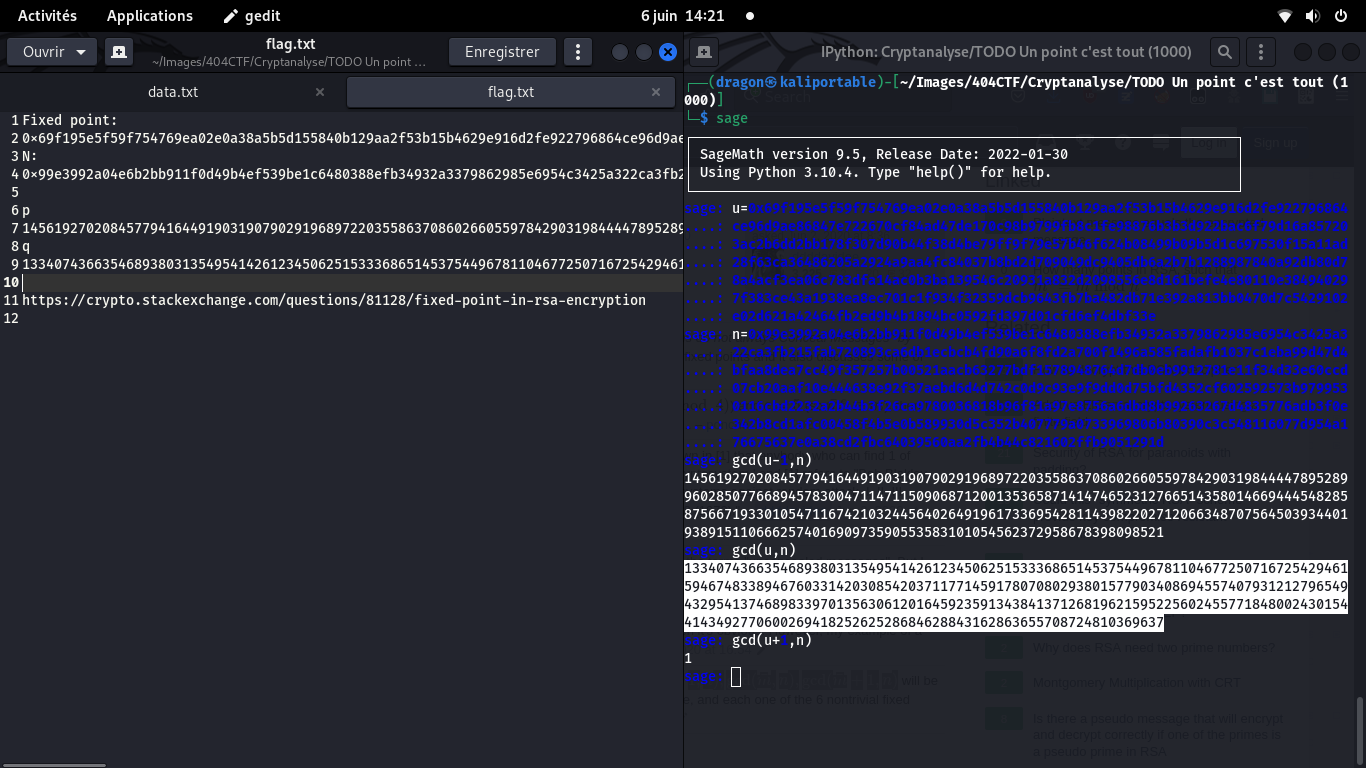
D'où GCD(u=k*P,N=P*Q) = P (vu que k < Q),
GCD(u+/-1,N) = Q car u+/-1 = {-1+1;1-1} mod Q = 0 mod Q, multiple de Q
et GCD(u-/+1,N) = 1 car u-/+1 = {-2,2} mod Q et u-/+1 = {0-1;0+1} mod P = {-1;1} mod P
n'est alors multiple ni de P ni de Q
La même approche s'applique aux autres points non-triviaux
(les autres combinaisons de {0;-1;1} mod {P;Q})
Le +/-1 précédent est choisi comme l'opposé de u mod Q: si u mod Q = -1 alors on prend +1 sinon on prend -1;
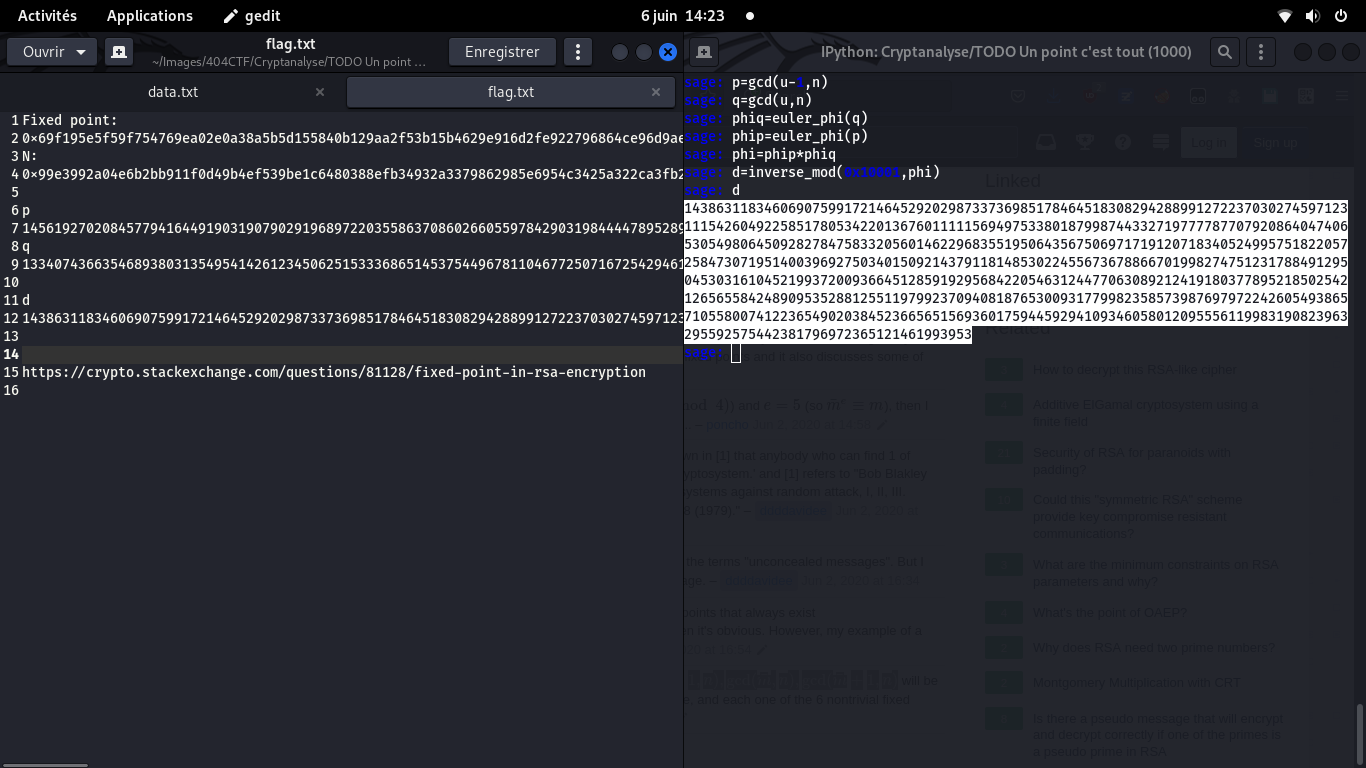
Sachant que N = P * Q, le calcul de phi(N) revient à calculer phi(P) * phi(Q), ce qui est nettement plus rapide et réalisable.
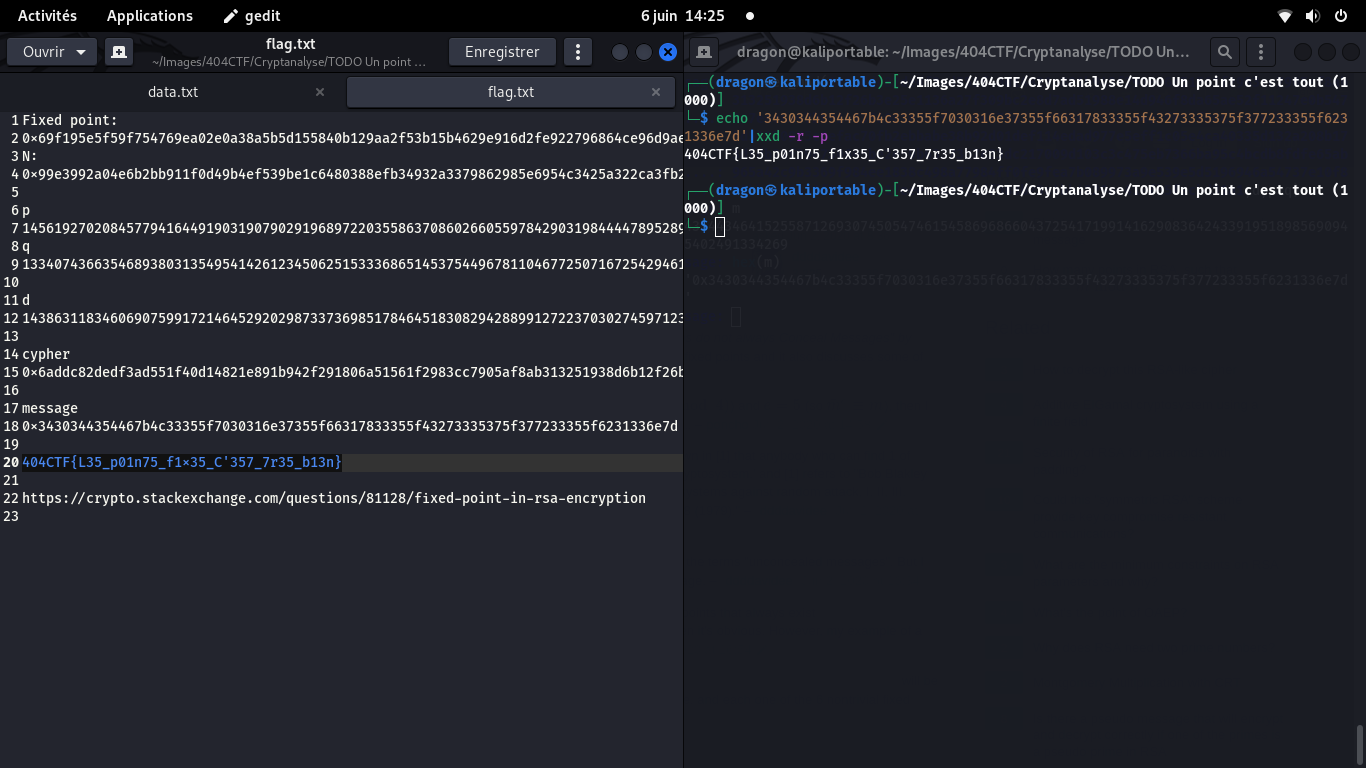
404CTF{L35_p01n75_f1x35_C'357_7r35_b13n}