(1-x)^n*(1+n*x)
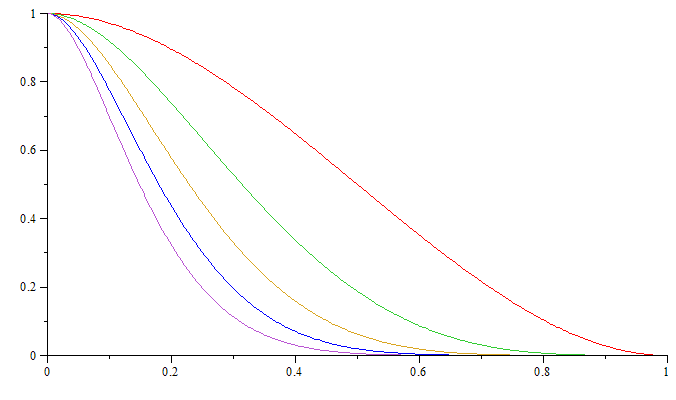
Demi-dôme, plus nn est grand,
plus la pente est raide près de x = 0
nvitesse de "chute" du dômex ∈ [0..1] → [0..1], f(0) = 1, f(1) = 0f'(x) = -n * (n+1) * x * (1-x)^(n-1), f'(0) = f'(1) = 0
(1-x)^n * (1+n*x), n ∈ [0;1]
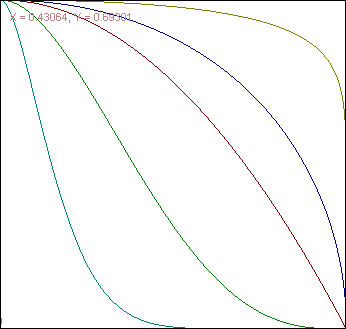
Différentes valeurs de n (n→0 en jaune, n=1 en bleu, n>1 en vert)
x ∈ [0;1] → [0;1], f(0) = 1, f(1) = 0f'(x) = [ (1-x)^n*(1+n)*n*x ] / (x-1)f'(0) = 0, ∀n, f'(1) = +∞, n>=1, f'(1) = 0, n<1max(f'(x)) = f'(1/n)
1/2 * (x^n + x^(1/n) )
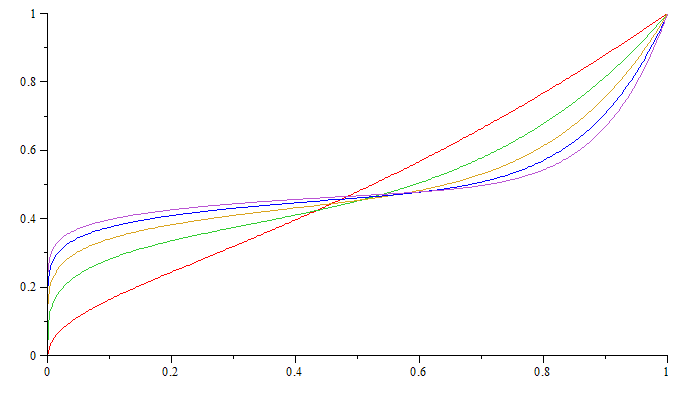
Plus n > 1 est grand, plus le plat est marqué
x ∈ [0..1]-
f'(x) = (n²*x^n + x^(1/n)) / (2*n*x)(non dérivable enx=0)
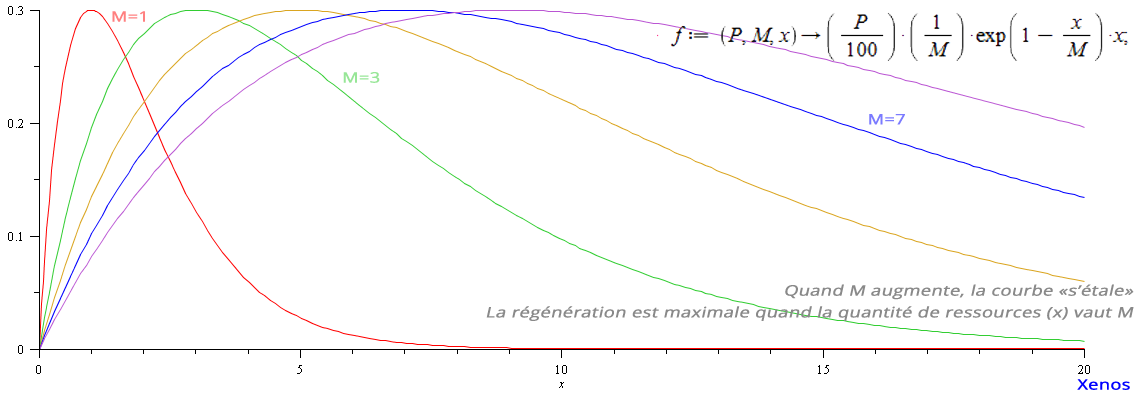
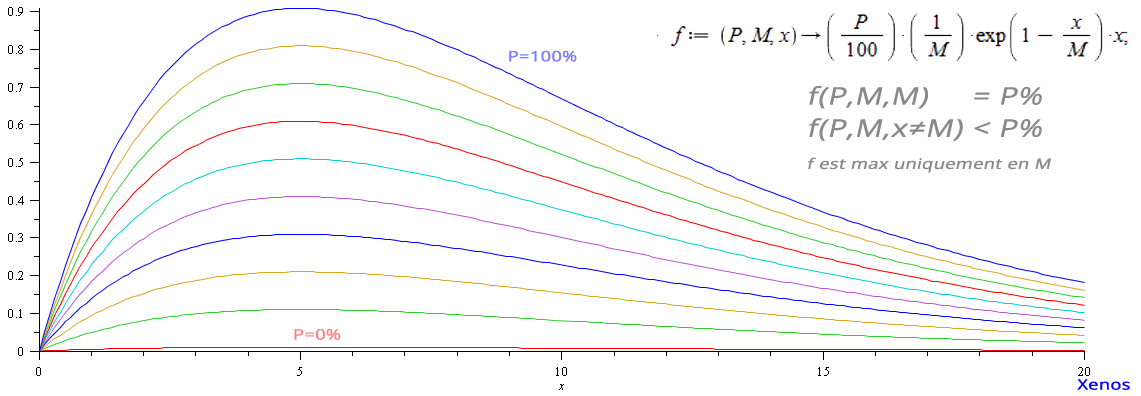
(P/100)*(1/M)*exp(1-x/M)*x
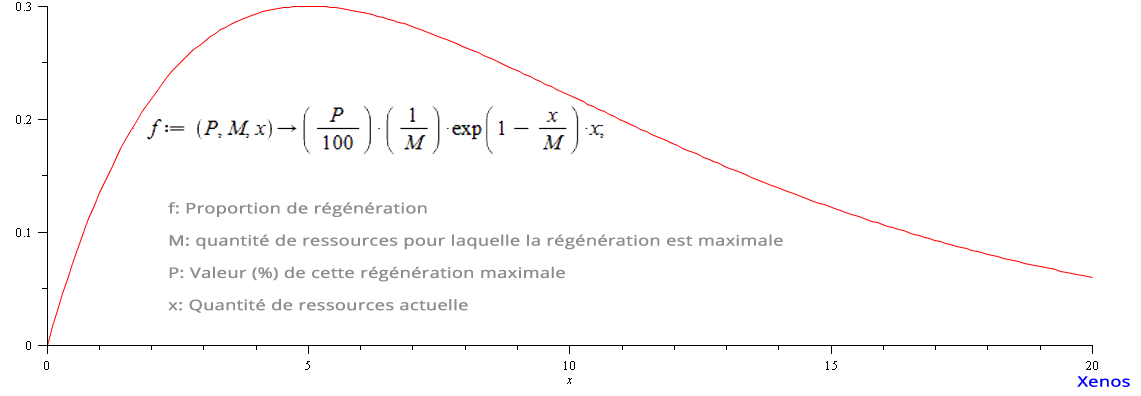
Maximale en x = M,
et f(M) = P/100
f(0) = 0, f(M) = P%, f(x!=M) < P%f'(x) = (P/100) * (1/M) * exp(1-x/M) * (1 - x/M)f'(M) = 0, f'(0) = (P/100) * (1/M) * exp(1)
0.5 * ( tan(2*k*x-k)/tan(k) + 1 )
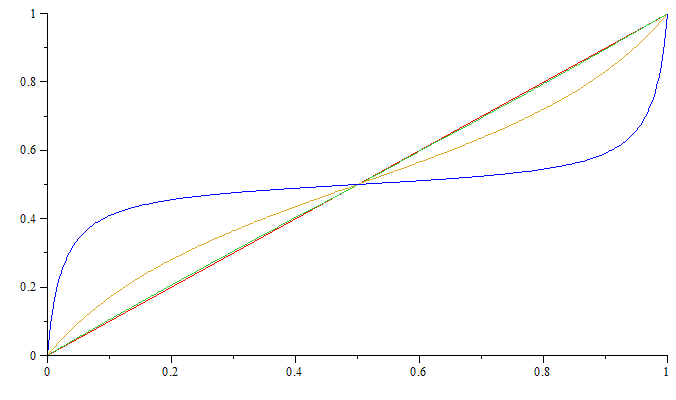
Fonction de 0 à 1, avec un "plat" plus ou moins marqué en 0.5
-
De
k=0(pas de plat) àk≈Pi/2(courbe très plate) x ∈[0..1] → [0..1], f(0) = 0, f(1) = 1a > b ⇔ f(a) > f(b)(croissance stricte)-
xn'apparait qu'une fois dansf(x)(pratique si x vautrand())
ln(cosh( (x-a)/b )) + x/c
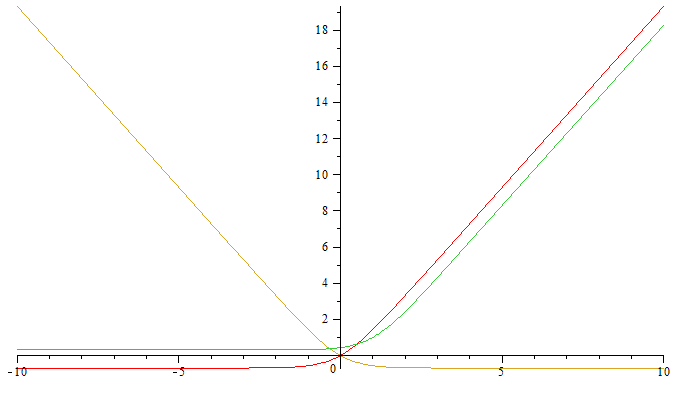
La fonction présente deux asymptotes; la valeur de b en
détermine la pente.
- La courbe présente deux asymptotes linéaires en +∞ et -∞
-
Pour
a=b*ln(2)etc=b,fest 'plate' de -∞ à 0, et linéaire au-delà de 0. Plusbest grand, plus la pente est raide. -
f'(x) = 1/b * tanh( (x-a)/b ) - 1/c -
f(-∞) = a/b - ln(2)(sib=c) -
f(+∞)/x ≈ 1/b - 1(poura = b*ln(2))
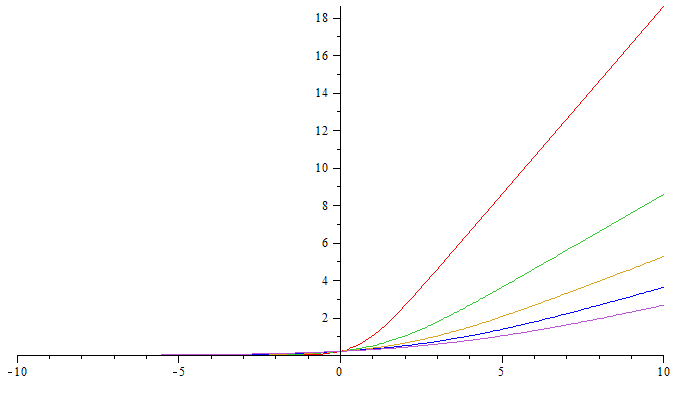
Régression barycentrique
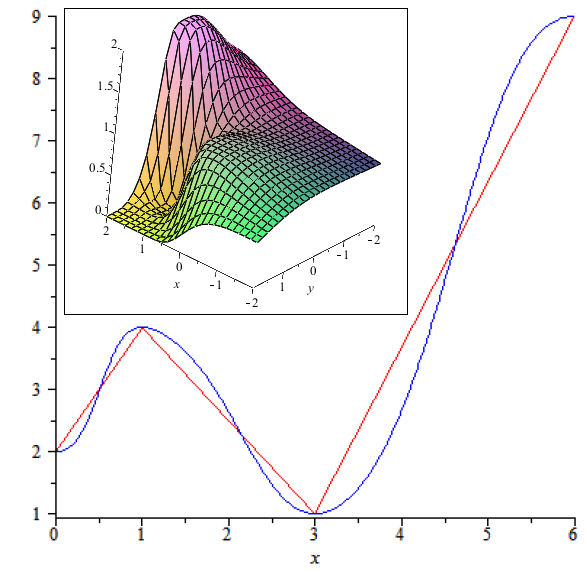
Une méthode personnelle permettant de définir une courbe (surface, volume, etc) passant par tous les points d'une liste donnée (2D, 3D, 4D ou plus) et de la "lisser" selon le résultat que l'on souhaite atteindre
Triangle approché
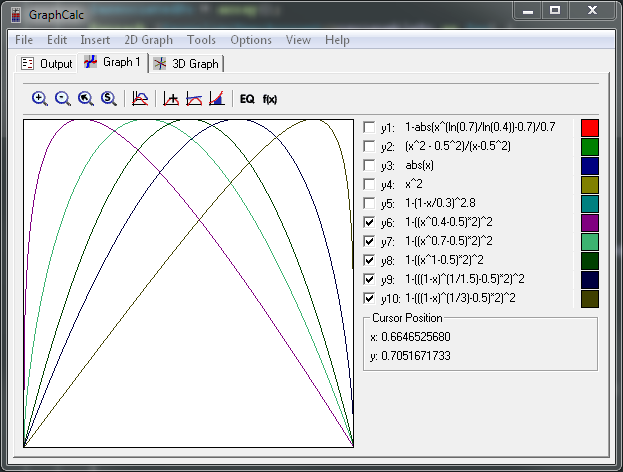
0.5>A>0
k = ln(0.5)/ln(A)
f(x, k<1, n ∈ N*) = 1-(2*(x^k - 0.5))^(2*n)
1>A>0.5
k = ln(1-A)/ln(0.5),
f(x, k>1, n ∈ N*) = 1-(2*((1-x)^(1/k) - 0.5))^(2*n)
Une fonction "à peu près" en triangle sur x ∈ [0..1],
maximale en x=A, f(A)=1.
Probablement trop complexe pour être utilisable